von Michael Himmelbauer

Bereits in der Unterstufe lernt man, dass ein Stromkreis aus Stromquellen und Verbrauchern* bestehen kann. Ein Beispiel für einen Verbraucher ist eine Glühlampe.

Mehrere Glühlampen kann man in einem Stromkreis beliebig anordnen, genauer gesagt in Serien- und Parallelschaltung.

Für unseren Versuch braucht man sieben Glühlampen, die man folgendermaßen (auf einem Steckbrett) anordnet:

An den beiden Schaltungen wird nun dieselbe Spannung angelegt. Es wird davon ausgegangen, dass die sieben Glühlampen gleich sind.

Wir möchten nun herausfinden, welche der beiden rechten Glühlampen (oben und unten) heller leuchtet:

A) Die obere rechte Glühlampe leuchtet heller.

B) Beide rechten Glühlampen leuchten gleich hell.

C) Die untere rechte Glühlampe leuchtet heller.

Wie findet man das heraus?

Um vorgehen zu können, müssen wir die Glühlampen als Widerstände betrachten und uns an die Formeln zur Berechnung von Widerständen in Serien- und Parallelschaltungen erinnern:

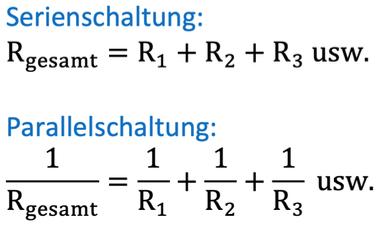
Damit wir etwas über die Spannung, die an der jeweils rechten Glühlampe anliegt, herausfinden, müssen wir zunächst den jeweils linken Teil der Schaltkreise betrachten. Außerdem nehmen wir an, dass jede Glühlampe den Widerstand x hat.

Der Widerstand des linken Teils der oberen Schaltung ist einfach x, da es sich nur um einen einzigen Widerstand handelt.

Bei der unteren Schaltung müssen wir die Formeln für die Serien- und dann für die Parallelschaltung verwenden:

Der Widerstand in der unteren Schaltung ist also auch x, das bedeutet, dass an beiden rechten Glühlampen dieselbe Spannung anliegen müsste und sie damit gleich hell leuchten müssten, es wäre also Antwort B richtig.

Nun schalten wir den Strom ein und kommen zu folgendem Ergebnis:

Die vier Glühlampen im linken Teil des unteren Stromkreises leuchten logischerweise weniger hell, da sich die Spannung in der Serienschaltung der einzelnen Stränge der Parallelschaltung „aufteilt“.

Zu Beginn leuchten tatsächlich auch die beiden rechten Glühlampen gleich hell, doch dann stellt sich heraus, dass die untere rechte Glühlampe etwas heller leuchtet als die obere.

Doch warum ist das so?

Eine Glühlampe hat innen in der „Glaskugel“ einen Glühdraht, der sich beim Leuchten erwärmt.

Dadurch, dass die linke Glühlampe im oberen Stromkreis viel heller leuchtet als die vier linken Glühlampen im unteren Stromkreis, hat diese mit der Zeit auch einen höheren Widerstand, obwohl es im unteren Stromkreis vier Glühlampen sind, diese leuchten allerdings kaum.

Und warum hat ein warmer Glühdraht einen höheren Widerstand als ein kalter?

Das ist dadurch zu erklären, dass sich, wenn der Draht (in diesem Fall durch den Stromfluss) erwärmt wird, die freien Elektronen im Metallgitter mehr zu bewegen beginnen, wodurch der Strom mehr Widerstand beim „Durchfließen“ hat.

Bei längerem Betrieb des Stromkreises ist somit Antwort C richtig.

Zusammenfassend ist zu sagen, dass der Widerstand einer Glühlampe von der Helligkeit und der Betriebsdauer abhängt.

(*) Das Wort Verbraucher wird zwar im Alltag gerne benutzt, ist aber physikalisch nicht korrekt. Tatsächlich wird von zum Beispiel einer Glühbirne keine Energie verbraucht, sondern die elektrische Energie in eine andere Energieform (bei der Glühbirne in Wärmeenergie) umgewandelt. Korrekt wäre somit statt Verbraucher: Energieumwandler